Nama : Timothy Gilbert
NIM : 2301851036
Hari: Selasa 9 Juni 2020
Kelas : CB01-CL
Lecturer : Ferdinand Ariandy Luwinda(D4522), Henry Chong (D4460)
Hal yang akan dibahas pada pertemuan kali ini :
1. AVL tree concept
2. Rebalance AVL Tree
1. AVL tree concept
Pada AVL tree kita harus memperhatikan balance factor tiap node yang ada pada tree tersebut. Balance factor pada tiap node di dalam tree tidak boleh kurang dari -1 dan tidak boleh lebih dari 1. Cara untuk mendapatkan balance factor yaitu dengan menggunakan rumus
balance factor = jumlah path terpanjang anak kiri - jumlah path terpanjang anak kanan.
Cara untuk menginsert data dan untuk mendelete data pada AVL tree ini sama seperti cara untuk menginsert data dan mendelete data pada Binary Search Tree. Akan tetapi dikarenakan tree pada Binary Search Tree memungkinkan terjadinya suatu ketidak seimbangan tree, maka diciptakannyalah AVL tree, yang bertujuan untuk menyeimbangkan tree pada Binary Search Tree.
2. Rebalance AVL tree
Dikarenakan Binary Search Tree memiliki kemungkinan terjadi ketidak seimbangan pada tree, maka setiap kali kita menginsert data ataupun kita mendelete suatu data, kita harus seimbangkan treenya dengan menggunakan AVL tree, dengan cara menggunakan rumus balance factor.
Terdapat 2 kasus pada saat kita merebalance avl tree yaitu :
1. single rotation
ada 2 kemungkinan kasus yang harus diselesaikan dengan single rotation yaitu:
1. the deepest node is located at the left sub tree of the child of T
contoh :
pada tree seperti itu kita harus melakukan rebalancing dengan cara LL rotation
2. the deepest node is located at the right sub tree of the child of T
contoh:
pada tree seperti itu kita harus melakukan rebalancing dengan cara RR rotation
ada 2 kemungkinan kasus yang harus diselesaikan dengan double rotation
1. the deepest node is located at the right sub tree of the left child of T
contoh :
pada tree seperti itu kita harus melakukan rebalancing dengan cara RL rotation
2. the deepest node is located at the left sub tree of the right child of T
contoh :
pada tree seperti itu kita harus melakukan rebalancing dengan cara LR rotation
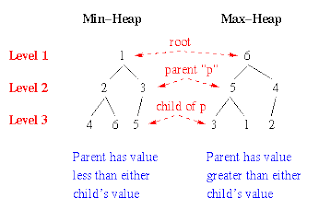
Heap
heap merupakan sebuah Complete Binary Tree yang memenuhi persyaratan heap.
secara umum heap terbagi menajdi 2 yaitu: Min Heap dan Max Heap.
Min heap merupakan heap dengan nilai parent yang lebih kecil dari pada childrennya.
Max heap merupakan heap dengan nilai parent yang lebih besar dari pada childrennya
contohnya :
kegunaan dari heap yaitu Heap itu gunanya untuk menemukan nilai max untuk max heap, dan min untuk min heap. dan ini sangat berguna pada saat membuat Priority Queue.
Heaps are usually implemented in an array. And root is sorted at index 1
example:
cara untuk mencari parent sm child tinggal masukin rumus:
Index_Parent=Index/2;
Index_Child_Kiri=Index*2;
Index_Child_kanan=Index*2+1;
Index_Parent=Index/2;
Index_Child_Kiri=Index*2;
Index_Child_kanan=Index*2+1;
Insertion
untuk insertion baik pada min heap dan max heap sama saja, akan tetapi hanya berbeda pada tanda penunjuk lebih besar atau lebih kecilnya saja.
insertion pada min heap
Saat sebuah data baru dimasukkan dalam heap, maka data langsung ditempatkan di index terakhir dalam heap. Setelah itu, data di-upheap. Maksudnya, data dibandingkan dengan parentnya. Bila lebih kecil, maka swap dengan parentnya. Hal ini dilakukan sampai data tersebut lebih besar dari parentnya.
contoh:
ternyata 1<51. Maka, 1 dan 51 di swap. Begitu pula dengan saat 1 dibandingkan dengan 50 dan dengan 2.

maka tampilan akhir dari heap kita akan menjadi sebagai berikut
untuk insertion pada max heap kebalikan dari min heap tetapi caranya sama saja hanya dibalik pembadingnya saja
Deletion
Jika dalam insertion dipakai Upheap, maka dalam deletion dipakai Downheap. Deletion dalam heap otomatis menghapus node root dari heap. Jadi, delete min dalam min heap dan delete max dalam max heap.
Dalam deletion, node paling akhir langsung menggantikan root yang didelete. Kemudian, node tersebut langsung di downheap sampai ke posisinya.
contoh:
Node 1 pada gambar dibawah ini yang berperan sebagai root langsung dihapus dalam deletion.
node 51 sebagai data paling akhir langsung naik menjadi root . Node tersebut akan di-downheap; ditukar dengan min(LeftChild, RightChild) bila node < min(LeftChild, Right Child)Sehingga min heap tersebut akan menjadi seperti gambar disamping.
Tries
Kata trie adalah infiks dari kata "retrieval" karena trie dapat menemukan satu kata dalam kamus dengan hanya awalan kata. Gagasan utama dari struktur data trie terdiri dari bagian-bagian berikut:
•Tries is a tree where each vertex represents a single word or a prefix.
•The root represents an empty character (‘’).
•A vertex that are k edges of distance from the root have an associated prefix of length k.
•Let a and b be two vertices of the tries and assume a is a direct parent of b, then b must have an associated prefix of a.
Contoh dari tries sebagai berikut:
contoh dari tries yang memuat kata : “tree”, “trie”, “algo”, “assoc”, “all”, and “also.”
sumber:
ppt Binus pert 12 mei
http://apalah-ini-itu.blogspot.com/2011/06/heap.html
https://www.topcoder.com/community/competitive-programming/tutorials/using-tries/
https://www.topcoder.com/community/competitive-programming/tutorials/using-tries/